There is a bi-directional graph with n vertices, where each vertex is labeled from 0 to n - 1 (inclusive). The edges in the graph are represented as a 2D integer array edges, where each edges[i] = [ui, vi] denotes a bi-directional edge between vertex ui and vertex vi. Every vertex pair is connected by at most one edge, and no vertex has an edge to itself.

You want to determine if there is a valid path that exists from vertex source to vertex destination.

Given edges and the integers n, source, and destination, return true if there is a valid path from source to destination, or false otherwise.

Example 1:

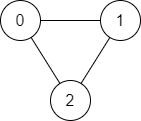
Input: n = 3, edges = [[0,1],[1,2],[2,0]], source = 0, destination = 2
Output: true
Explanation: There are two paths from vertex 0 to vertex 2:
- 0 → 1 → 2
- 0 → 2

Example 2:

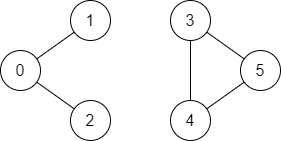
Input: n = 6, edges = [[0,1],[0,2],[3,5],[5,4],[4,3]], source = 0, destination = 5
Output: false
Explanation: There is no path from vertex 0 to vertex 5.

<解題>

1. 建立一個used的boolean陣列，來記錄哪些節點已被使用。
2. 一開始，起點 start 被標記為已使用，並將 newUsedFound 設置為 true，並使用一個迴圈來尋找從起點到終點的路徑。
3. 在每次迴圈中，程式遍歷 edges 數組中的每個邊，檢查邊的兩個節點是否有其中一個已被使用。
4. 如果其中一個節點已被使用，則將另一個節點標記為已使用，並將 newUsedFound 設置為 true。

class Solution {
    public boolean validPath(int n, int[][] edges, int start, int end) {
        boolean[] used = new boolean[n];
        used[start] = true;
        boolean newUsedFound = true;
        while (!used[end] && newUsedFound) {
            newUsedFound = false;
            for (int i = edges.length - 1; i >= 0; i--) {
                if (used[edges[i][0]]) {
                    if (!used[edges[i][1]])  newUsedFound = used[edges[i][1]] = true;
                } else if (used[edges[i][1]]) {
                    newUsedFound = used[edges[i][0]] = true;
                }
            }
        }
        return used[end];
    }
}

Time: O(E)->邊的數量 Space: O(n)->boolean[] used = new boolean[n];