PattySung

You are given an m x n integer matrix matrix with the following two properties:

Each row is sorted in non-decreasing order. The first integer of each row is greater than the last integer of the previous row. Given an integer target, return true if target is in matrix or false otherwise.

You must write a solution in O(log(m * n)) time complexity.

Example 1:

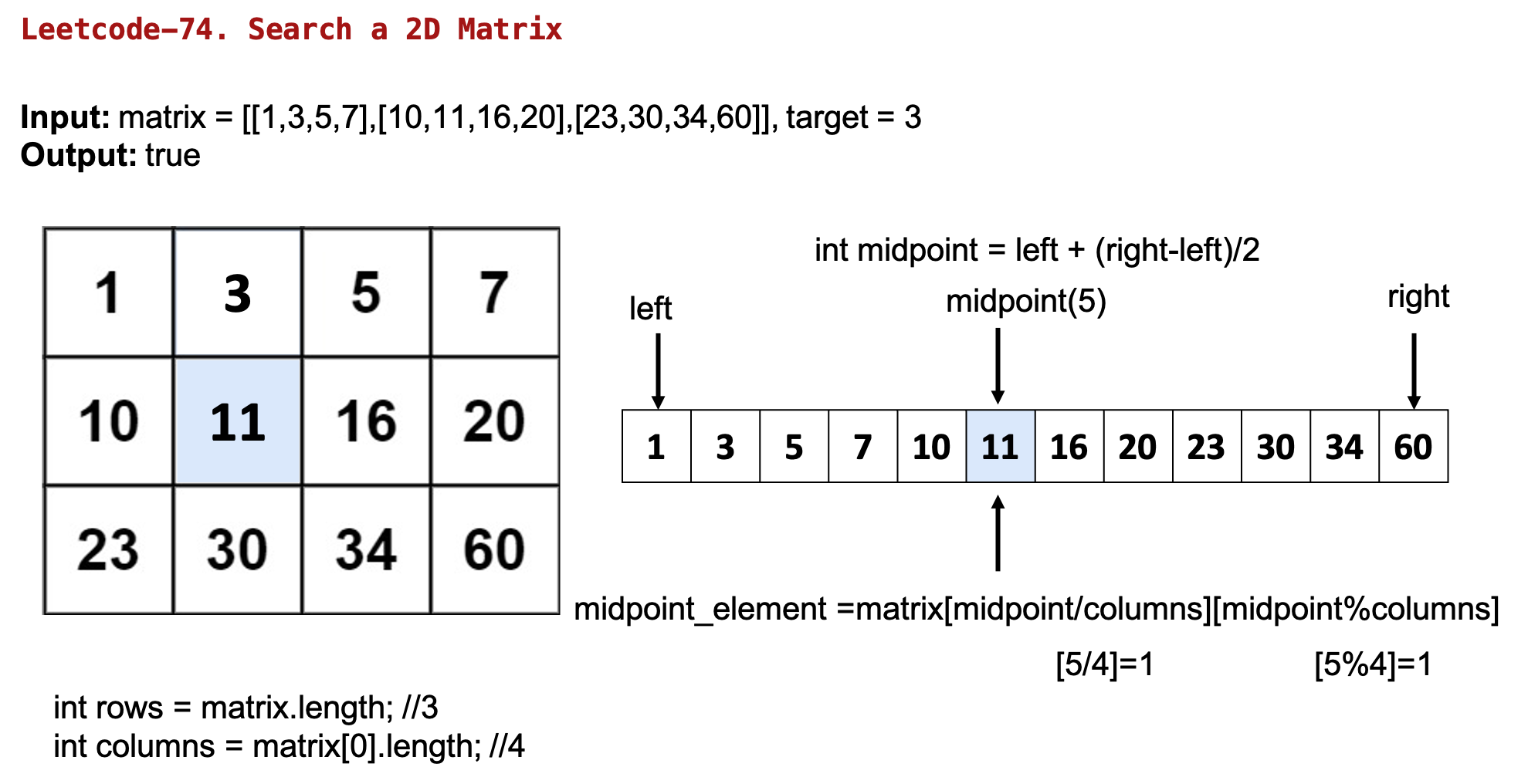
Input: matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
Output: true

Example 2:

Input: matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13
Output: false

<解題>

這題和過往的BST類似，差別在於其為2D matrix，所以在index上需要作轉換
用midpoint 去找是否和target相同，而每次的midpoint更新，需要同時將index轉成matrix[][]的形式：

int midpoint_element = matrix[midpoint/columns][midpoint%columns];


class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        if(matrix == null) return false;

        int rows = matrix.length;
        int columns = matrix[0].length;
        int left = 0;
        int right = rows * columns -1;

        while (left <= right){
            int midpoint = left + (right -left)/2; //一般BST作法
            int midpoint_element = matrix[midpoint/columns][midpoint%columns]; //轉換成matrix裡面的index ->index==5，要換成[1,1]
            if(midpoint_element == target){
                return true;
            } else if(target < midpoint_element){
                right = midpoint-1;
            } else if(target > midpoint_element){
                left = midpoint+1;
            }
        }
        return false;
    }
}

Time: O(log(mn)) ->mn為矩陣的行列數

Space: O(1)

Leetcode-74. Search a 2D Matrix

<解題>